Answer with Explanation:
We are given that
Resistance of solenoid,R=4.3 ohm
Magnetic field,B=

Current,I=4.6 A
Diameter of wire,d=0.5 mm=
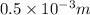
Radius of wire,r=

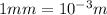
Radius of solenoid,r'=1 cm=

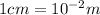
Resistivity of copper,

We know that
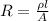
Where
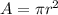
Using the formula

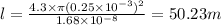
Number of turns of wire=
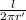
Number of turns of wire=
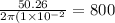
Hence, the number of turns of the solenoid,N=799
Magnetic field in solenoid,B=

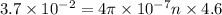

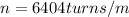
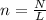
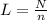
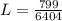
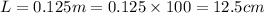
Length of solenoid=12.5 cm
1m=100 cm