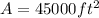Question

You have 600 feet of fencing to enclose a rectangular plot that borders on a river. If you do not fence the side along the river, find the length and width of the plot that will maximize the area. What is the largest area that can be enclosed?

Answer 1

The length and width of plot is
`L=300\:ft`,
`W=150\:ft`

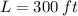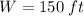
Largest area of the plot is
`A=45000 ft^(2)`

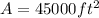
Explanation:

Assume width as x and length as y. Given that length of fencing is 600 feet and fencing is enclosed on 3 sides. So perimeter is given as,

Perimeter = width + length + width

Substituting the value,

`600=x+y+x`

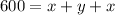
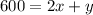`600= 2x+y` ….1

Now area of fence of rectangular box is given as follows,

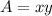`A=xy` ….2

Solving equation 1 for y, subtracting 2x from both sides,

`600-2x= y`

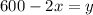
Substituting the value in equation 2,

`A=x\left (600-2x  \right )`

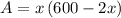
Simplifying

`A=600x-2x^(2)`

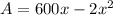
Rewriting,

`A=-2x^(2)+600x`

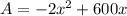
Above equation looks like quadratic equation
`f\left ( x \right )=ax^(2)+bx+c` whose graph looks like parabola.

Comparing equation f(x) and A values of a, b and c are,
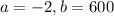`a=-2,b=600` and
`c=0`.

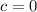Now maximum of
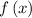`f\left ( x \right )` occurs at vertex.

The x coordinate of the vertex is given as
`-(b)/(2a)`

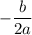
Substituting the values,

`x=-(600)/(2\left (-2  \right ))`

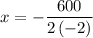
Simplifying,

`x=(600)/(4)`

`x=150`

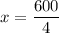
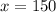
So width of plot is 150 feet.

Now to calculate value of length by using equation 1,

`600= 2x+y`

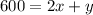
Substituting the values,

`600= 2\left (150  \right )+y`

`600= 300+y`

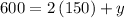
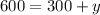
Subtracting 300 from both sides,

`300= y`

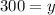
So length of plot is 300 ft.

The y coordinate of the vertex is given as
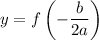`y=f\left ( -(b)/(2a) \right )` which also means,
`y=f\left ( 150 \right )`

`\therefore A=-2\left (150  \right )^(2)+600\left (150  \right )`

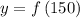
Simplifying,

`\therefore A=-2\left (22500  \right )^(2)+600\left (150  \right )`

`\therefore A=-45000+90000`

`\therefore A=45000`

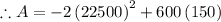
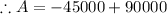
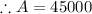
So, area of the plot will be
`A=45000 ft^(2)`