Question

A box is sliding down an incline tilted at a 11.6° angle above horizontal. The box is initially sliding down the incline at a speed of 1.10 m/s. The coefficient of kinetic friction between the box and the incline is 0.390. How far does the box slide down the incline before coming to rest?

Answer 1

0.34 m

Step-by-step explanation:

We are given that

`\theta=11.6^(\circ)`

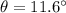
Initial speed of box=u=1.1 m/s

Coefficient of friction,
`\mu=0.39`

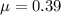
We have to find the distance slide down by the box before coming to rest.

Friction force=f=
`\mu mg=`

Where
`g=9.8 m/s^2`

Net force=
`mgsin\theta-\mu mg`

`ma=mg(sin\theta-\mu cos\theta)`

`a=g(sin\theta-\mu cos\theta)`

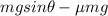
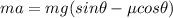
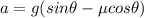
Substitute the values

`a=9.8(sin11.6-0.39cos11.6)=9.8(-0.18)=-1.76 m/s^2`

`v=0`

`v^2-u^2=2as`

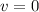
Substitute the values

`0-(1.1)^2=2(-1.76)s`

`-3.52s=-(1.1)^2`

`s=(-(1.1)^2)/(-3.52)`

`s=0.34 m`

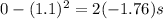
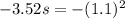
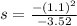
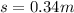
Hence, the box slide down the incline 0.34 m before coming to rest.