Answer:
The average fill in the soup cans is different than the claimed amount of 16 ounces.
Explanation:
A one-sample t-test can be used to test whether the population mean is significantly different from some hypothetical value of 16 ounces or not.
The hypothesis is:
H₀: The average fill in the soup cans is 16 ounces, i.e. µ = 16.
Hₐ: The average fill in the soup cans is different from 16 ounces, i.e. µ ≠ 16.
Assume that the significance level of the test is α = 0.05.
The t-statistic is given by,
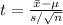
Here
 = sample mean = 15.8 ounces
= sample mean = 15.8 ounces
s = sample standard deviation = 0.9 ounces
n = sample size = 101.
Compute the value of the test statistic as follows:
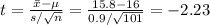
The calculated t-statistic is, t = -2.23 which follows t-distribution with (n-1) = 100 degrees of freedom.
Decision rule:
If the p-value of the test statistic is less than the significance level α then the null hypothesis will be rejected. And if the p-value is more than α then the null hypothesis will not be rejected.
The p-value is,
p-value = 0.028.
Use the p-value from t-score calculator.
The calculated p-value, p = 0.028 < α = 0.05.
The null hypothesis will be rejected at 5% level of significance.
Conclusion:
The average fill in the soup cans is different than the claimed amount of 16 ounces.