Question

A car weighs 2200 lb and is travelling 100 mi/h on a race track that is on a 3% upgrade. The car is preparing to pass a slower car and its torque/engine speed curve is given by (with Me in ftlb and ne in revolutions per second): Me = 8ne - 0.05n; Drivetrain efficiency is 90%, drive axle slippage is 2%, wheel radius is 15 inches, frontal area is 22 ft2, drag coefficient is 0.35, and air density is 0.0022 slugs/ft3. If the car is in a gear that produces maximum torque, what would the car's maximum acceleration be?

Answer 1

- 0.3275 ft / s^2 cars maximum acceleration

Step-by-step explanation:

The average drag force is calculated as

fo = 1/2 ∝ A
`v^(2)` α

α = drag coefficient = 0.35

∝ = 1.328

A = 22 ft^2 = 2.04387 m^2

S = 0.0022 slugs/ft3 = 1.1338 kg/m^3

V = 100 m/h = 44.704 m/s

fo = 1/2 * 1.328 * 2.04387 *
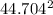`44.704^(2)` * 0.35

= 81044 N

next calculate the torque/engine speed curve

Me = 8ne - 0.05 *
`ne^(2)`

ne = 4800 rev /min = 80 rev /sec

Me = 8.80 - 0.05 * 80 ^2

= 320 Ib ft = 438.86 Nm

next calculate torque at the curve

= torque speed * drive train efficiency * 1 - drive axle slippage

= 433.86 * 0.9 * 0.98

= 382.66 N-m

force at the wheel ( F wheel) = 1004.368 N

radius = 15 in = 0.381 m

the opposing forces to this are drag force and weight along the upgrade

race track given = 0.03

which means the angle ∅ can be gotten from tan ∅ = 0.03 or ∅ = 1.71835

car mass = 2200 Ib = 997.9032 kg

to calculate the car's maximum acceleration we apply newton's second law

A max = F wheel - Fo - mg sin∅

1004.368 - 810.44 - 997.9032 * 9.8 * sin ∅

= 997.9032 Ra

= a = -0.09983 m/s^2

= - 0.3275 ft / s^2

Answer 2

Detailed solution is given below: