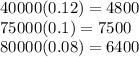Question

A man has $195,000 invested in three properties. One earns 12%, one 10% and one 8%. His annual income from the properties is $18,700 and the amount invested at 8% is twice that invested at 12%.

(a) How much is invested in each property?
12% property $
10% property $
8% property $

(b) What is the annual income from each property?
12% property $
10% property $
8% property $

Answer 1

`40000(0.12) = 4800\\75000(0.1) = 7500\\80000(0.08) = 6400`Answer:

Explanation:

Given that a man has $195,000 invested in three properties. One earns 12%, one 10% and one 8%. His annual income from the properties is $18,700 and the amount invested at 8% is twice that invested at 12%.

12% 10% 8% total

Principal x y z 195000

Interest 0.12x 0.1y 0.08z 18700

z=2x

Thus we get three equations as

x+y+z = 195000: 0.12x+0.1y+0.08z = 18700 and z =2x

substitute z value in first 2 equations to get

3x+y = 195000: 0.28x+0.1y = 18700 or 28x+10y =1870000

30x+10y =1950000

2x = 80000 or x = 40000

3(40000)+y = 195000: y = 75000

z = 80000

a) How much is invested in each property?

12% property $ ... 40000

10% property $ ... 75000

8% property $ ... 80000

b) Annual income =