Question

Suppose a 0.034 M aqueous solution of sulfuric acid (H2SO4) is prepared. Calculate the equilibrium molarity of (SO4)^2-.

Answer 1

Answer: The concentration of
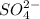`SO_4^(2-)` at equilibrium is 0.0068 M

Step-by-step explanation:

As, sulfuric acid is a strong acid. So, its first dissociation will easily be done as the first dissociation constant is higher than the second dissociation constant.

In the second dissociation, the ions will remain in equilibrium.

We are given:

Concentration of sulfuric acid = 0.034 M

Equation for the first dissociation of sulfuric acid:

`H_2SO_4(aq.)\rightarrow H^+(aq.)+HSO_4^-(aq.)`

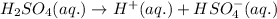
0.034 0.034 0.034

Equation for the second dissociation of sulfuric acid:

`HSO_4^-(aq.)\rightarrow H^+(aq.)+SO_4^(2-)(aq.)`

Initial: 0.034 0.034

At eqllm: 0.034-x 0.034+x x

The expression of second equilibrium constant equation follows:

`Ka_2=([H^+][SO_4^(2-)])/([HSO_4^-])`

We know that:

`Ka_2\text{ for }H_2SO_4=0.0102`

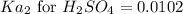
Putting values in above equation, we get:

`0.0102=((0.034+x)* x)/((0.034-x))\\\\x=-0.051,0.0068`

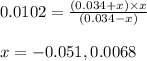
Neglecting the negative value of 'x', because concentration cannot be negative.

So, equilibrium concentration of sulfate ion = x = 0.0068 M

Hence, the concentration of
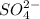`SO_4^(2-)` at equilibrium is 0.0068 M