Question

A plate falls vertically to the floor and breaks up into three pieces, which slide along the floor. Immediately after the impact, a 400-g piece moves along the x-axis with a speed of 2.00 m/s and a 430-g piece moves along the y-axis with a speed of 1.50 m/s. The third piece has a mass of 100 g. In what direction does the third piece move?

Answer 1

The direction from negative x direction will be 38.87° .

Step-by-step explanation:

Given data

The masses of the plates pieces and their velocity is given as follows

m₁= 400 g u=2.00 i m/s

m₂=430 g v= 1.50 j m/s

m₃=100 g

let takes the final velocity of mass m₃ = w

by using conservation of linear momentum as follows

initial momentum =final momentum

(m₁+ m₂+ m₃) x V = m₁ u + m₂ v + m ₃w

The initial velocity of the system is zero ,that is why V= 0 m/s

Now by putting the values in the above equation

( 930 g) x 0 = 400 x 2 i + 430 x 1.5 j + 100 x w

100 w= - 800 i - 645 j

w = - 8 i - 6.45 j

The direction of velocity of mass m₃ is given as follows

`tan\theta=(-6.45)/(-8)`

`\theta = 38.87^(\circ)`

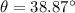
Therefore the direction from negative x direction will be 38.87° .

Answer 2

Step-by-step explanation:

m1 = 400 g

v1 = 2 m/s along X axis = 2i

m2 = 430 g

v2 = 1.5 m/s along Y axis = 1.5 j

m3 = 100 g

Let the velocity of third part is v.

Use conservation of momentum

initial momentum = 0

So final momentum is also equal to zero.

m1 x v1 + m2 x v2 + m3 x v = 0

400 x 2i + 430 x 1.5 j + 100 x v = 0

100 v = - 800 i - 645 j

v = - 8 i - 6.45 j

Let the direction is θ.

tanθ = 6.45 / 8

θ = 219° from X axis