Question

Linear Time Invariant Systems For each of the systems below an input x(t) and the output y(t) are plotted. Determine whether each of these are linear time invariant (LTI) systems, and can be described by a convolution. Provide an argument for your answer. Note that some cases are described in the time domain, and some in the frequency domain.

Answer 1

The system can be described by a convolution

Step-by-step explanation:

Thinking process:

If we consider a discrete input to a linear time-invariant system, then the system will be periodic with respect to the period, say N. This therefore, means that the output must also be periodic. The proof is as follows:

The LTI system can be written for the system where:

y (n+N) = ∑
`h(k)x(n + N - k)`

= ∑
`h(k)x(n-k)\\= y(n)`

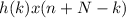
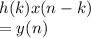
From the proof, it turns out that y(y + N) = y(n) for any value of n, then the output will be the periodic with the period N.