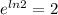Question

If g(x) is the inverse of f(x), what is the value of f(g(2))?

Answer 1

The answer is C on edge 2020

2

Explanation:

I just took the Quiz

Answer 2

2

Explanation:

So to figure this out we just need to flip the values of x and y in the table and then redefine that as the function g(x), because an inverse is essentially the reverse!

So if we flipped x and y's for f(x). We would see that our output or y of g(x) is -3 when x = 2, or in other words g(2) = -3. This means that we are now going to solve for when f(-3). So now lets look at the table and find the value at x = -3 for f(x). This value is 2, so the value of f(g(2)) = 2.

*In the future*

When you have a composite function of two inverses they essentially cancel out and would leave whatever the value of x is. So if we know f(x) and g(x) were inverses the value of f(g(2)) would just be 2.

For example:

ln(x) and e^x are inverses so if I had a composition like this:

`e^(ln(2))`

The answer to this would be 2 because these inverse functions "'cancel" out

So

`e^(ln2) = 2`