Question

In classical physics, consider a 2 kg block hanging on a spring with a spring constant of 50 N/m. Ignore air resistance. The block is held with the spring stretched 14 cm from its hanging equilibrium position. At t = 0 the block is let go. After the block evolves dynamically for 0.9 s, an ideal measurement is made of the block's speed. What is the result of this measurement (in cm/s)? Answer to one decimal place.

Answer 1

v = 0

Step-by-step explanation:

This problem can be solved by taking into account:

- The equation for the calculation of the period in a spring-masss system

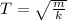`T = \sqrt{(m)/(k) }` ( 1 )

- The equation for the velocity of a simple harmonic motion

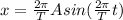`x = (2\pi )/(T)Asin((2\pi )/(T)t)` ( 2 )

where m is the mass of the block, k is the spring constant, A is the amplitude (in this case A = 14 cm) and v is the velocity of the block

Hence

`T = \sqrt{(2 kg)/(50 N/m)} = 0.2 s`

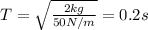
and by reeplacing it in ( 2 ):

`v = (2\pi )/(0.2s)(14cm)sin((2\pi )/(0.2s)(0.9s)) = 140\pi sin(9\pi ) = 0`

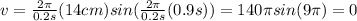
In this case for 0.9 s the velocity is zero, that is, the block is in a position with the max displacement from the equilibrium.