Question

The base of the 37 foot ladder is 9 feet from the wall of a building. will the top of the ladder reach a window ledge 35 feet above the ground?

-I know its a yes but what is the math in it?

Answer 1

You have to use the Pythagorean theorem. the formula is A squared + B squared = C squared. The formula with the numbers plugged in would look like this. 9 squared + ? = 37 squared. When we simplify it will be 81 + B squared = 1369. Now we have to subtract 81 from both sides so the equation will be 81 - 81 = B squared = 1369 - 81. 1369 - 81 is 1288. The square root of 1288 is 25 so the answer is correct.

Explanation:

Answer 2

Yes

Explanation:

Use the Pythagorean theorem!

So if we have a 37 foot ladder propped up the side of the building then 37 ft would be the hypotenuse. If the ladder is 9 feet away from the building that would be one leg of our triangle, and the other leg would be how much the ladder reaches up the side of the building.

So if we solve for the missing side of this triangle we will find how far up the ladder can reach. So using pythagoras:

`9^(2) + b^(2) = 37^(2)`

`81 + b^(2) = 1369`

`b^(2) = 1288`

`b = √(1288)`

`b = 35.88`

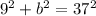
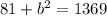
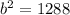
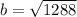
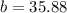
So the ladder reaches up 35.88 ft meaning that it would reach a window ledge 35 feet above the ground.