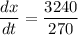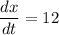Answer:
The value of rate at which the sales are changing is 12
Explanation:
Given function is,
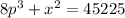
To determine the rate at which sales are changing, that is,
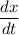 , differentiate given function with respect to t,
, differentiate given function with respect to t,
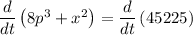
Applying sum rule of derivative,
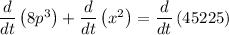
Applying power rule and constant rule of derivative,
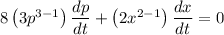
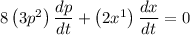
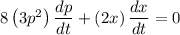
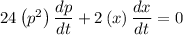
Substituting the values,
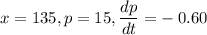
Since it is given that price is falling, so
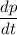 is negative.
is negative.
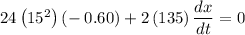
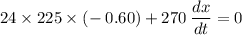
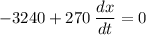
Adding -3240 from both sides,
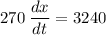
Dividing by 270,