Question

I need help on this exercise

Answer 1

The length of PR is 16 inches.

Solution:

PQR is a triangle and ST is the mid-segment of ΔPQR.

Given ST = 8 inches

By triangle mid-segment theorem,

The segment connecting the mid-points of two sides of a triangle is parallel to the third side and is half of the length of that side.

`\Rightarrow ST || PR \ \text{and} \ ST=(1)/(2) PR`

`$\Rightarrow S T=(1)/(2) P R`

`$\Rightarrow 8=(1)/(2) P R`

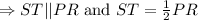
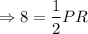
Multiply by 2 on both sides.

`$\Rightarrow 8* 2=2* (1)/(2) P R`

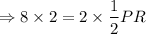
⇒ 16 = PR

The length of PR is 16 inches.