Question

Picture explains
asdasdasd

Answer 1

AB is tangent to the circle

Explanation:

The tangent of a circle is always perpendicular (at a right angle) to the radius. Therefore, if AB is the tangent to the circle, the angle between the radius and AB will be 90° (and ΔBAO will be a right triangle).

Pythagoras Theorem

`a^2+b^2=c^2`

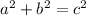
where:

• a and b are the legs of the right triangle
• c is the hypotenuse (longest side) of the right triangle

Given:

• a = 12
• b = 16
• c = 20

Substitute the given values into the formula:

`\implies 12^2+16^2=20^2`

`\implies 144+256=400`

`\implies 400=400`

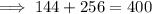
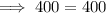
Therefore, as ΔBAO is a right triangle with ∠BAO = 90°, AB is tangent to the circle.

Answer 2

• Yes, AB is tangent

Explanation:

The tangent is perpendicular to the radius. The given triangle is right if AB is tangent.

Use Pythagorean to verify

• 20² = 16² + 12²
• 400 = 256 + 144
• 400 = 400

Confirmed