Answer:
The time required for the magnetic field to decrease to zero from its maximum value is
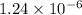 sec.
sec.
Step-by-step explanation:
Given :
Magnetic field
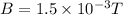
No. of turns
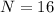
Area of loop
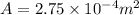
Average emf
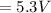
From the faraday's electromagnetic induction principle,
Average emf
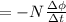
Where
 change in magnetic flux,
change in magnetic flux,
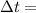 change in time.
change in time.
The magnetic flux is given by,
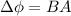
In our example, we have to find time required to decrease magnetic field so our above equation is modified as,
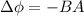
 for decrease in magnetic field.
for decrease in magnetic field.
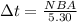
Where
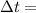 time required for the magnetic field to decrease to zero from its maximum value
time required for the magnetic field to decrease to zero from its maximum value
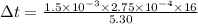
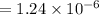 sec.
sec.