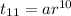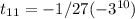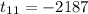Question

The 3rd term of a geometric sequence is -1/3 and the 8th term is 81. what is the 11th term?

Answer 1

Answer:
`t_(11)=-2187`

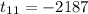
Explanation:

`t_(3)=-1/3`

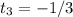
That is :

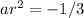`ar^(2) = -1/3` ................. equation 1

Also

`t_(8)=81`

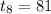
that is

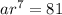`ar^(7)=81` ................. equation 2

divide equation 2 by equation 1 , that is

`(ar^(7))/(ar^(2)) = 81 / -1/3`

`r^(5)=`
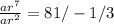
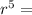
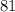`81` x
`-3/1`

`r^(5)= -243`

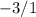
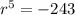
find the fifth root of both sides

`r = -3`

substitute
`r = -3` , into equation 1 to find a , that is

`a(-3^(2))= -1/3`

`9a = -1/3`

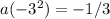
multiply through by 3

`27a = -1`

`a =- 1/27`

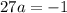
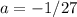
To find the 11th term , the formula for the 11th term is given as :

`t_(11)=ar^(10)`

`t_(11)= -1/27(-3^(10))`

`t_(11)=-2187`