Answer:
Therefore it will take
 s for the object to reach the ground.
s for the object to reach the ground.
Explanation:
Given function is
H(t) = -64 t²+169.
where H is height in feet, and t is time in second.
When the object touches the ground, the height of the object will be zero.
i.e H(t) = 0.
Therefore
H(t) = 0
⇒ -64 t²+169=0
⇒ -64 t²= -169

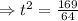
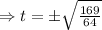 [ square root both sides]
[ square root both sides]
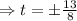
Time can not be negative.
Therefore
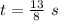
Therefore it will take
 s for the object to reach the ground.
s for the object to reach the ground.