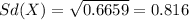Answer:
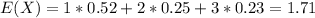
Now we can calculate the second moment with the following formula:
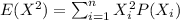
And replacing we got:
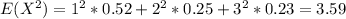
And the variance is given by:
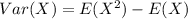
And replacing we got:
![Var(X) = 3.59 -[1.71]^2 = 0.6659](https://img.qammunity.org/2021/formulas/mathematics/college/rcd1tittsny0hzx0i06shfbqtwwh5d1ywg.png)
And the standard deviation is just the square root of the variance:
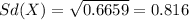
Explanation:
Previous concepts
For this case we define the random variable X =" how many children the couple will have" and we know the following distribution:
X 1 2 3
P(X) 0.52 0.250 0.230
The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.
The variance of a random variable X represent the spread of the possible values of the variable. The variance of X is written as Var(X).
Solution to the problem
For this case we can find the expected value with the following formula:
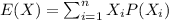
And replacing we got:
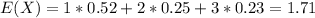
Now we can calculate the second moment with the following formula:
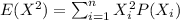
And replacing we got:
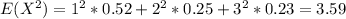
And the variance is given by:
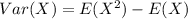
And replacing we got:
![Var(X) = 3.59 -[1.71]^2 = 0.6659](https://img.qammunity.org/2021/formulas/mathematics/college/rcd1tittsny0hzx0i06shfbqtwwh5d1ywg.png)
And the standard deviation is just the square root of the variance: