Step-by-step explanation:
The given data is as follows.
 = (19 + 273) K = 292 K,
= (19 + 273) K = 292 K,
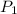 = 1.0 atm,
= 1.0 atm,
 = 1.4 L
= 1.4 L
Therefore, moles of gas present will be calculated as follows.
n =
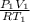
=
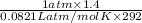
=
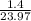
= 0.058 mol
Since, neon is a monoatomic ideal gas hence, expression for its constant volume heat capacity is as follows.
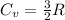
As the gas is expanding to a volume (
 ) of 2.8 L and it is heated to
) of 2.8 L and it is heated to
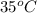 or (35 + 273) K = 308 K.
or (35 + 273) K = 308 K.
So, entropy change for this reaction will be calculated as follows.
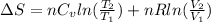
=

=
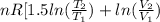
=

=
![0.4822 * [1.5 * 0.052 + 0.693]](https://img.qammunity.org/2021/formulas/chemistry/college/kt9c9arlc83qy5u5orrrshwbfkrpb23bu4.png)
= 0.372 J/K
Thus, we can conclude that the entropy change for the process is 0.372 J/K.