Answer:
(a) The distribution of (Y - X) is N (0.001, 0.0005).
(b) The probability that the pin will not fit inside the collar is 0.023.
Explanation:
The random variable X is defined as the diameter of the pin and the random variable Y is defined as the diameter of the collar.
The distribution of X and Y is:

The random variables X and Y are independent of each other.
(a)
Compute the expected value of (Y - X) as follows:
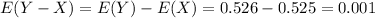
The mean of (Y - X) is 0.001.
Compute the variance of (Y - X) as follows:
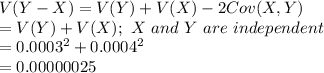
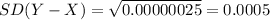
The standard deviation of (Y - X) is 0.0005.
Thus, the distribution of (Y - X) is N (0.001, 0.0005).
(b)
Compute the probability of [(Y - X) ≤ 0] as follows:
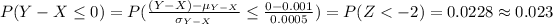
*Use a z-table for the probability value.
Thus, the probability that the pin will not fit inside the collar is 0.023.