Question

The clearance between a pin and the collar around it is important for the proper performance of a disc drive for small computers. The specifications call for the pin to have diameter 0.525 centimeter (cm) and for the collar to have diameter 0.526 cm. The clearance will then be 0.001 cm. In practice, both diameters vary from part to part independently of each other. The diameter X of the pin has the N(0.525, 0.0003) distribution, and the distribution of the diameter Y of the collar is N(0.526, 0.0004). a) What is the distribution of the clearance Y-X? b) What is the probability P(Y-X  0) that the pin will not fit inside the collar?

Answer 1

(a) The distribution of (Y - X) is N (0.001, 0.0005).

(b) The probability that the pin will not fit inside the collar is 0.023.

Explanation:

The random variable X is defined as the diameter of the pin and the random variable Y is defined as the diameter of the collar.

The distribution of X and Y is:

`X\sim N(0.525, 0.0003)\\Y\sim N(0.526, 0.0004)`

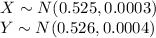
The random variables X and Y are independent of each other.

(a)

Compute the expected value of (Y - X) as follows:

`E(Y-X)=E(Y)-E(X)=0.526-0.525=0.001`

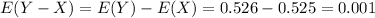
The mean of (Y - X) is 0.001.

Compute the variance of (Y - X) as follows:

`V(Y-X)=V(Y)+V(X)-2Cov(X,Y)\\=V(Y)+V(X);\ X\ and\ Y\ are\ independent\\=0.0003^(2)+0.0004^(2)\\=0.00000025`

`SD(Y-X)=√(0.00000025)=0.0005`

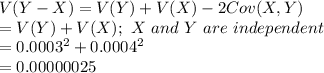
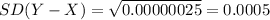
The standard deviation of (Y - X) is 0.0005.

Thus, the distribution of (Y - X) is N (0.001, 0.0005).

(b)

Compute the probability of [(Y - X) ≤ 0] as follows:

`P(Y-X\leq 0)=P(((Y-X)-\mu_(Y-X))/(\sigma_(Y-X))\leq (0-0.001)/(0.0005))=P(Z<-2)=0.0228\approx0.023`

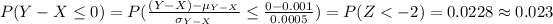
*Use a z-table for the probability value.

Thus, the probability that the pin will not fit inside the collar is 0.023.