Answer:
(a). The value of temperature at the end of heat addition process
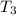 = 2042.56 K
= 2042.56 K
(b). The value of pressure at the end of heat addition process
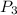 = 1555.46 k pa
= 1555.46 k pa
(c). The thermal efficiency of an Otto cycle
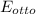 = 0.4478
= 0.4478
(d). The value of mean effective pressure of the cycle
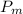 = 1506.41
= 1506.41
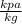
Step-by-step explanation:
Compression ratio
 = 8
= 8
Initial pressure
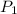 = 95 k pa
= 95 k pa
Initial temperature
 = 278 °c = 551 K
= 278 °c = 551 K
Final pressure
 = 8 ×
= 8 ×
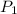 = 8 × 95 = 760 k pa
= 8 × 95 = 760 k pa
Final temperature
 =
=
 ×
×
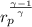
Final temperature
 = 551 ×
= 551 ×
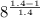
Final temperature
 = 998 K
= 998 K
Heat transferred at constant volume Q = 750
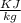
(a). We know that Heat transferred at constant volume
 =
=
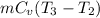
⇒ 1 × 0.718 × (
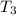 - 998 ) = 750
- 998 ) = 750
⇒
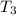 = 2042.56 K
= 2042.56 K
This is the value of temperature at the end of heat addition process.
Since heat addition is constant volume process. so for that process pressure is directly proportional to the temperature.
⇒ P ∝ T
⇒
 =
=

⇒
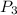 =
=
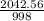 × 760
× 760
⇒
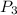 = 1555.46 k pa
= 1555.46 k pa
This is the value of pressure at the end of heat addition process.
(b). Heat rejected from the cycle
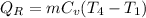
For the compression and expansion process,
⇒
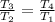
⇒
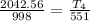
⇒
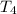 = 1127.7 K
= 1127.7 K
Heat rejected
 = 1 × 0.718 × ( 1127.7 - 551)
= 1 × 0.718 × ( 1127.7 - 551)
⇒
 = 414.07
= 414.07
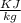
Net heat interaction from the cycle
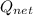 =
=
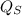 -
-

Put the values of
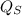 &
&
 we get,
we get,
⇒
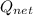 = 750 - 414.07
= 750 - 414.07
⇒
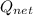 = 335.93
= 335.93
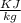
We know that for a cyclic process net heat interaction is equal to net work transfer.
⇒
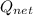 =
=
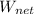
⇒
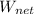 = 335.93
= 335.93
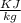
This is the net work output from the cycle.
(c). Thermal efficiency of an Otto cycle is given by
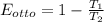
Put the values of
 &
&
 in the above formula we get,
in the above formula we get,
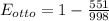
⇒
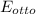 = 0.4478
= 0.4478
This is the thermal efficiency of an Otto cycle.
(d). Mean effective pressure
 :-
:-
We know that mean effective pressure of the Otto cycle is given by
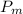 =
=
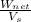 ---------- (1)
---------- (1)
where
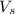 is the swept volume.
is the swept volume.
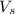 =
=
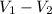 ---------- ( 2 )
---------- ( 2 )
From ideal gas equation
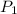
 = m × R ×
= m × R ×

Put all the values in above formula we get,
⇒ 95 ×
 = 1 × 0.287 × 551
= 1 × 0.287 × 551
⇒
 = 0.6
= 0.6

From the same ideal gas equation

 = m × R ×
= m × R ×

⇒ 760 ×
 = 1 × 0.287 × 998
= 1 × 0.287 × 998
⇒
 = 0.377
= 0.377

Thus swept volume
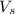 = 0.6 - 0.377
= 0.6 - 0.377
⇒
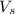 = 0.223
= 0.223

Thus from equation 1 the mean effective pressure
⇒
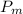 =
=
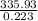
⇒
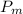 = 1506.41
= 1506.41
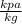
This is the value of mean effective pressure of the cycle.