Question

An altitude is drawn from the vertex of an isosceles triangle, forming a right angle

and two congruent triangles. As a result, the altitude cuts the base into two equal
segments. The length of the altitude is 18 inches, and the length of the base is
17
inches. Find the triangle's perimeter. Round to the nearest tenth of an inch.

Answer 1

Answer:56.8 inches

Explanation:

For perimeter we must find the lengths of the 2 diagonal sides of the triangle which are the same because it is isosceles.

the triangle is cut directly in half so both halves of the base are 17/2

17/2 = 8.5

solve through pythagoren theorum

altitude^2 + (half of base)^2 = (diagonal length)^2

18^2 + (8.5)^2 = (diagonal length)^2

324 + 72.25 = (diagonal length)^2

396.3 = (diagonal length)^2

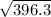`√(396.3)` = diagonal length

diagonal length = 19.9

diagonal length + diagonal length + base = perimeter

19.9 + 19.9 + 17 = perimeter

56.8 inches = perimeter