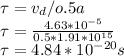Answer:
a)Drift velocity,
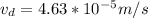
Electric field in the wire, E = 1.083 * 10⁴ V/m
b)
Step-by-step explanation:
a) Diameter of the wire, d = 1.0 mm = 0.001 m
Area of the wire, A =

A =

A = 0.000000785 m² = 7.85 * 10^-7
Current carried by the wire, I = 0.50 A
Number density of the conduction electrons, n = 8.5 * 10²⁸ m⁻³
charge of an electron, e = 1.62 * 10⁻¹⁹C
Current,
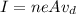 , where
, where
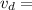 Drift velocity
Drift velocity
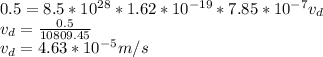
Resistivity,
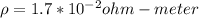
Electric field,
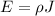
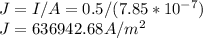
E = 1.7 * 10⁻² * 636942.68
E = 1.083 * 10⁴ V/m
b) If an electron moves with constant acceleration,
S = v t.............(1)
If the electron starts from rest
S = 0.5 at².........(2)
Equating (1) and (2) and making
 and v =
and v =
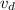

To get the value of a
F = qE and F= ma
qE = ma
a = qE/m
Mass of an electron, m = 9.1 * 10⁻³¹kg
a = (1.602 * 10⁻¹⁹*1.083 * 10⁴)/(9.1*10⁻³¹)
a = 1.91 * 10¹⁵m/s²