Question

CO(g) + Cl2 (g) ⇌ COCl2 (g) Kp = 22.5 at 395 °C . A sample of COCl2 (g) is introduced into a constantvolume vessel at 395 °C and observed to exert an initial pressure of 0.351 atm. When equilibrium is established, what will be the total pressure within the vessel?

Answer 1

`P_T=0.456atm`

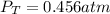
Step-by-step explanation:

Hello,

In this case, it is convenient to rewrite the chemical reaction considering the COCl₂ as the reactant, so we must invert the equilibrium constant as shown below:

`Kp'=(1)/(Kp) =(p_(CO)^(eq)p_(Cl_2)^(eq))/(p_(COCl_2)^(eq))=0.0444`

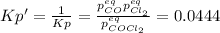
Thus, by introducing the change
`x` due to reaction's progress, one obtains:

`0.0444=(x^2)/(0.351-x)`

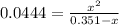
Solving for
`x` via quadratic equation or solver, one obtains:

`x_1=-0.149atm\\x_2=0.105atm`

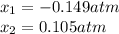
Clearly, the solution is
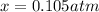`x=0.105atm` for which the total pressure at equilibrium is:

`P_T=p_(CO)^(eq)+p_(Cl_2)^(eq)+p_(COCl_2)^(eq)=0.105atm+0.105atm+(0.351atm-0.105atm)\\P_T=0.456atm`

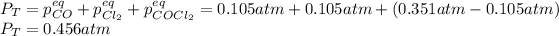
Best regards.