Question

A point charge of -2.10 �C is located in the center of a spherical cavity of radius 6.54 cm inside an insulating spherical charged solid. The charge density in the solid is 7.36 x 10-4 C/m3. Calculate the electric field inside the solid at a distance of 9.48 cm from the center of the cavity. (magnitude and direction)

Answer 1

`-3.4* 10^5 N/C`

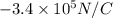
Step-by-step explanation:

We are given that

`q_0=-2.1\mu C=-2.1* 10^(-6) C`

`1\mu C=10^(-6) C`

`r_1=6.5 cm=6.54* 10^(-2) m`

`1 m=100 cm`

`r_2=9.48 cm=9.48* 10^(-2) m`

`\rho=7.36* 10^(-4) C/m^3`

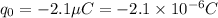
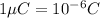
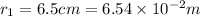
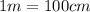
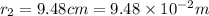
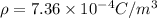
We have to find the electric field inside the solid at distance of 9.48 cm from the center of the cavity.

Volumetric charge density,
`\rho=(Q)/(V)`

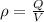
Charge on spherical solid=
`Q=V\rho=(4)/(3)\pi(r^3_2-r^3_1)\rho`

`Q=(4)/(3)\pi((9.48* 10^(-2))^3-(6.54* 10^(-2))^3)* 7.36* 10^(-4)=1.76* 10^(-6) C`

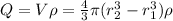
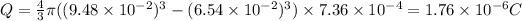
Electric field =Electric field due to spherical charge solid +electric field due to charge at center

`E=(KQ)/(r^2)+(Kq_0)/(r^2)=(k)/(r^2)(Q+q_0)`

Where
`k=9* 10^9`

`E=(9* 10^9*)/((9.48* 10^(-2))^2)(1.76* 10^(-6)-2.1* 10^(-6))=-3.4* 10^5 N/C`

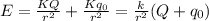
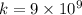
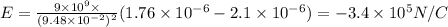
Where negative sign indicates that the direction of electric field is inward.