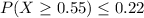Answer:
Explanation:
Using central Limit Theorem (CLT), The sum of 100 random variables;
 is approximately normally distributed with
is approximately normally distributed with
Y ~ N (100 ×
 ) = N ( 50,
) = N ( 50,
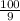 )
)
The approximate probability that it will take this child over 55 seconds to complete spinning can be determined as follows;
N ( 50,
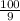 )
)
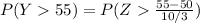
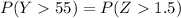
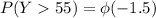
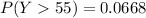
Using Chebyshev's inequality:
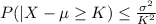
Let assume that X has a symmetric distribution:
Then:
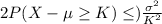
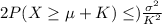
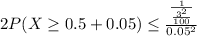 where: (
where: (
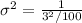 )
)