Question

One day, Karen bought 22 random cans of soup from a grocery store. Suppose that 5% of cans sold at that particular grocery store are dented, and assume the store's inventory is large enough that no individual customer's purchase affects the dent rate for the remaining cans. What is the probability that Karen has bought at least one dented can

Answer 1

Probability that Karen has bought at least one dented can is 0.6765.

Explanation:

We are given that Karen bought 22 random cans of soup from a grocery store. Suppose that 5% of cans sold at that particular grocery store are dented, and assume the store's inventory is large enough that no individual customer's purchase affects the dent rate for the remaining cans.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

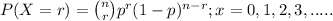
where, n = number of trials (samples) taken = 22 cans

r = number of success = at least one

p = probability of success which in our question is % cans sold at

that particular grocery store that are dented, i.e; 5%

LET X = Number of cans that are dented

So, it means X ~
`Binom(n=22, p=0.05)`

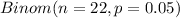
Now, Probability that Karen has bought at least one dented can = P(X
`\geq` 1)

P(X
`\geq` 1) = 1 - Probability that no cans are dented

= 1 - P(X = 0)

= 1 -
`\binom{22}{0}0.05^(0) (1-0.05)^(22-0)`

=
`1-(1 * 1 * 0.95^(22))`

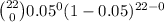
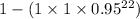
= 1 - 0.3235 = 0.6765

Therefore, Probability that Karen has bought at least one dented can is 0.6765.

Answer 2

0.6765 = 67.65%

Explanation:

This situation can be treated as a binomial model with probability of success (dented can) of p = 0.05.

In 22 random trials, the probability of at least one success is determined by:

`P(X>1) = 1-P(X=0)\\P(X>1) = 1 - (1-p)^(22)\\P(X>1) = 1 - (1-0.05)^(22)\\P(X>1) =0.6765`

The probability that Karen has bought at least one dented can is 0.6765 or 67.65%.