Question

Lucy kicks a shuttlecock into the air from a height of 0.6 feet

with an initial vertical velocity of 16 feet per second. Use the
vertical motion model, h = -16t2 + vt + s, where v is the
initial velocity in feet per second and s is the initial height in
feet, to calculate the maximum height of the shuttlecock.
Round your answer to the nearest tenth if necessary.
Maximum height: ___feet

Answer 1

4.6 feet

Explanation:

The equation is:

`h=-16t^2+vt+s`

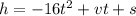
Where

v is initial velocity (given as 16)

s is initial height (given as 0.6)

Substituting, we can write:

`h=-16t^2+16t+0.6`

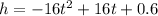
This is a quadratic equation of the general form:
`at^2+bt+c`

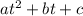
Which we can conclude the coefficients to be:

a = -16

b = 16

c = 0.6

The max height occurs at the value:
`t=-(b)/(2a)`

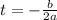
So, max height occurs at:

`t=-(16)/(2(-16))\\t=0.5`

We will get the max height if we put t = 0.5 into the original equation. So that would be:

`h=-16t^2+16t+0.6\\h=-16(0.5)^2+16(0.5)+0.6\\h=4.6`

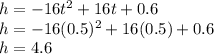
Max Height = 4.6 feet (occurs at t = 0.5 seconds)