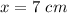Question

An open box is made from a 20​-cm by 50​-cm piece of tin by cutting a square from each corner and folding up the edges. The area of the resulting base is 216 cm2. What is the length of the sides of the​ squares?

Answer 1

7 cm

Explanation:

(20-2x)(50-2x) = 216

4x² - 40x - 100x + 1000 - 216 = 0

4x² - 140x + 784 = 0

x² - 35x + 196 = 0

x² - 28x - 7x + 196 = 0

x(x - 28) - 7(x - 28) = 0

(x - 7)(x - 28) = 0

x = 7, 28

x can not be more than 10 because the dimensions are 20×50

So x = 7 cm

Answer 2

Therefore,

The length of the sides of the​ squares is

`x=7\ cm`

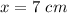
Explanation:

Let "x" be the length of Cut Square,

As the tin size(Dimension) is

20 cm × 50 cm

So the size(Dimension) of box will be

(20 - 2x) × (50 - 2x)

Length = 50 - 2x

Width = 20 - 2x

Area of base of box = 216 cm²

To Find:

x = ?

Solution:

Area of Rectangular field is given by

`(Area\ of\ Rectangle(Box)) = Length* Width`

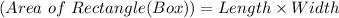
Substituting the values we get

`216=(50-2x)(20-2x)`

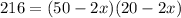
Applying Distributive property we get

`216=1000-100x-40x+4x^(2)`

`4x^(2)-140x+784=0`

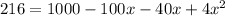
Dividing throughout by 4 we get

`x^(2)-35x+196=0`

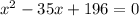
On Factorizing we get

`x^(2)-28x-7x+196=0\\\\(x-7)(x-28)=0\\\\x-7=0\ or\ x-28=0\\\\x=7\ or\ x = 28`

As x cannot be 28 because tin size is 20 cm × 50 cm i.e longer than 20

Therefore,

`x=7\ cm`

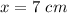
Therefore,

The length of the sides of the​ squares is

`x=7\ cm`