Step-by-step explanation:
First, we will calculate the entropies as follow.
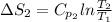 J/K mol
J/K mol
As,
 = 298 K,
= 298 K,
 = 373.8 K
= 373.8 K
Putting the given values into the above formula we get,
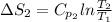 J/K mol
J/K mol
=
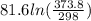
= 18.5 J/K mol
Now,
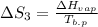
=
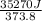
= 94.2 J/mol K
Also,

=

= 33.4 J/K mol
Now, we will calculate the entropy of one mole of methanol vapor at 800 K as follows.
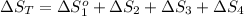
= (126.8 + 18.5 + 94.2 + 33.4) J/K mol
= 272.9 J/K mol
Thus, we can conclude that the entropy of one mole of methanol vapor at 800 K is 272.9 J/K mol.