Answer:
The distribution of proportion of people who will get the flu this winter is N (0.065, 0.014²).
Explanation:
Let X = number of people who will get flu this year.
The sample selected is of size, n = 309.
The number of people who will get flu in this sample is, x = 20.
Compute the sample proportion of people who will get flu as follows:
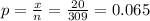
The random variable X follows a Binomial distribution with parameters n = 309 and p = 0.065.
The sample size is quite large, i.e. n = 309 > 30.
And the probability of success is low.
So the Normal approximation to Binomial can be used to approximate the distribution of sample proportion is:
- np ≥ 10
- n(1 - p) ≥ 10
Check whether the conditions are fulfilled or not as follows:
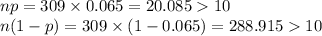
Hence, the conditions are fulfilled.
The sampling distribution of sample proportion is:
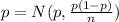
Compute the mean and variance as follows:
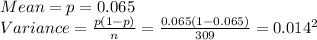
Thus, the distribution of proportion of people who will get the flu this winter is N (0.065, 0.014²).