Answer:
the proton will travel 0.074 m before reaching its turning point.
Step-by-step explanation:
Formula to calculate electric field because of the plate is as follows.
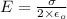
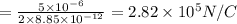
Now, we will consider that equilibrium of forces are present there. So,

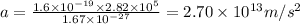
According to the third equation of motion,
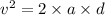

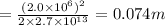
Thus, we can conclude that the proton will travel 0.074 m before reaching its turning point.