Question

An infinite plane has a surface charge density of -5.0 X 10-6 C/m2. A proton is shot straight away from the plane at 2.0 X 106 m/s. How far does the proton travel before reaching its turning point?

Answer 1

the proton will travel 0.074 m before reaching its turning point.

Step-by-step explanation:

Formula to calculate electric field because of the plate is as follows.

`E = (\sigma)/(2 * \epsilon_(o))`

`= (5 * 10^(-6))/(2 * 8.85 * 10^(-12)) = 2.82 * 10^(5) N/C`

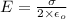
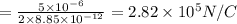
Now, we will consider that equilibrium of forces are present there. So,

`ma = qE`

`a = (1.6 * 10^(-19) * 2.82 * 10^(5))/(1.67 * 10^(-27)) = 2.70 * 10^(13) m/s^2`

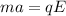
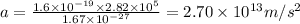
According to the third equation of motion,

`v^(2) = 2 * a * d`

`d = (v^(2))/(2d)`

`= ((2.0 * 10^(6))^(2))/(2 * 2.7 * 10^(13)) = 0.074 m`

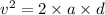
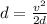
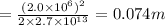
Thus, we can conclude that the proton will travel 0.074 m before reaching its turning point.

Answer 2

d = 0.07 m

Step-by-step explanation:

Given: σ = -5.0 × 10⁻⁶ C/m², v = 2.0 × 10⁶ m/s, ε = 8.85 × 10⁻¹² F/m,

Mass of Proton = 1.67 × 10⁻²⁷ kg and charge q = 1.60 × 10⁻¹⁹ C

Solution:

E = σ/2ε (for uniform field of large single plate)

E = -5.0 X 10⁻⁶ C/m² / (2 × 8.85 X 10⁻¹² F/m)

E = 2.82 × 10 ⁵ N/C

Now Work done = K.E.

F × d = 1/2 m v²

Eq × d = 1/2 m v²

d =m v² / 2Eq

d = 1.67 × 10⁻²⁷ kg (2.0 × 10⁶ m/s)² / 2 × 2.82 × 10 ⁵ N/C × 1.60 × 10⁻¹⁹ C

d = 0.07 m