Answer:
Therefore the solution of the differential equation is
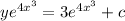 [ where c is arbitrary constant]
[ where c is arbitrary constant]
Explanation:
Given differential equation is
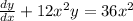
Here
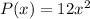 and
and
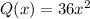
The integrating factor of the differential equation is
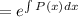
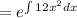


Multiplying the integrating factor both sides of the differential equation
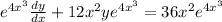
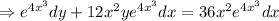
Integrating both sides,
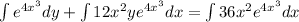 ......(1)
......(1)
Let
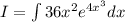
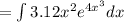
putting
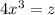 ,
,

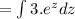
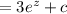 [ where c is arbitrary constant]
[ where c is arbitrary constant]
Putting the value of z
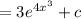
From (1) we get
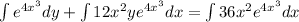
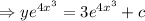
Therefore the solution of the differential equation is
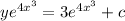 [ where c is arbitrary constant]
[ where c is arbitrary constant]