Question

A helicopter is flying at an altitude of 306 meters, at an angle of depression of 38° to its landing pad. What is the distance d between the helicopter and the landing pad? Round your answer to the nearest whole number.

Answer 1

497 m (nearest whole number)

Explanation:

As the problem has been modeled as a right triangle, we can use the sine trigonometric ratio to find the distance d.

Sine trigonometric ratio

`\sf \sin(\theta)=(O)/(H)`

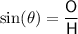
where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• H is the hypotenuse (the side opposite the right angle)

From inspection of the given diagram:

• 
  `\theta` = 38°
• O = 306 m
• H = d

Substitute the values into the formula and solve for d:

`\implies \sf \sin(38^(\circ))=(306)/(H)`

`\implies \sf H=(306)/(\sin(38^(\circ)))`

`\implies \sf H=497.0263891...`

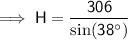
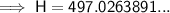
Therefore, the distance d between the helicopter and the landing pad is 497 m (nearest whole number).

Answer 2

• 497 m

Explanation:

Use tigonometry to find the value of d

• sine = opposite side / hypotenuse
• 306/d = sin 38°
• d =306/sin 38°
• d = 497 m (rounded)