Question

Line m passes through point (–2, –1) and is perpendicular to the graph of y = –23x + 6. Line n is parallel to line m and passes through point (4, –3). Which is the equation of line n in slope-intercept form?

Answer 1

`\huge\boxed{y=(1)/(23)x-(73)/(23)}`

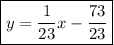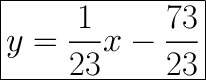
First, find the slope perpendicular to
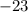`-23`. We can do this by finding the opposite reciprocal.

Multiply the slope by
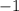`-1` and write the result as a fraction.

`-23*-1=23=(23)/(1)`

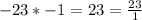
Flip the numerator and the denominator.

`(23)/(1)\longrightarrow(1)/(23)`

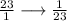
This is the slope of line
`m`. Since lines
`m` and
`n` are perpendicular, this is also the slope of line
`n`.

Write the formula for point-slope form.

`y-y_1=m(x-x_1)`

Substitute in the values for line
`n`.

`y-(-3)=(1)/(23)(x-4)`

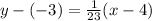
Simplify the negative subtraction.

`y+3=(1)/(23)(x-4)`

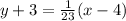
Distribute the
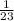`(1)/(23)` to the
`(x-4)`.

`y+3=(1)/(23)x-(4)/(23)`

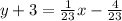
Subtract
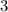`3` — which is equivalent to
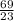`(69)/(23)` — from both sides.

`\boxed{y=(1)/(23)x-(73)/(23)}`