Question

A 15-ft ladder leans against a wall. The lower end of the ladder is being pulled away from the wall at the rate of 1.5 ft/sec. Let x be the distance from the bottom of the ladder to the wall, y be the distance from the top of the ladder to the ground and l be the length of the ladder. How fast is the top of the ladder moving along the wall at the instant it is 9 feet above the ground

Answer 1

The top of the ladder is sliding down at a rate of 2 feet per second.

Explanation:

Refer the image for the diagram. Consider
`\Delta ABC` as right angle triangle. Values of length of one side and hypotenuse is given. Value of another side is not known. So applying Pythagoras theorem,

`\left ( AB \right )^(2)+\left ( BC \right )^(2)=\left ( AC \right )^(2)`

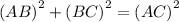
From the given data,
`L=15\:ft=AC`,
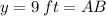`y=9\:ft=AB` and
`x=BC`

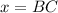
Substituting the values,

`\therefore \left ( 9 \right )^(2)+\left ( x \right )^(2)=\left ( 15 \right )^(2)`

`\therefore 81+x^(2)=225`

`\therefore x^(2)=225-81`

`\therefore x^(2)=144`

`\therefore \sqrt{x^(2)}=√(144)`

`\therefore x=\pm 12`

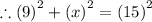
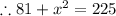
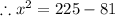
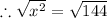
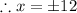
Since length can never be negative, so
`x= 12`.

Now to calculate
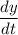`(dy)/(dt)` again consider following equation,

`\left ( y \right )^(2)+\left ( x \right )^(2)=\left ( l \right )^(2)`

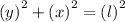
Differentiate both sides of the equation with respect to t,

`(d)/(dt)\left(y^2+x^2\right)=(d)/(dt)\left(l^2\right)`

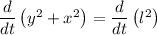
Applying sum rule of derivative,

`(d)/(dt)\left(y^2\right)+(d)/(dt)\left(x^2\right)=(d)/(dt)\left(l^2\right)`

`(d)/(dt)\left(y^2\right)+(d)/(dt)\left(x^2\right)=(d)/(dt)\left(225\right)`

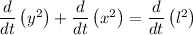
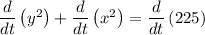
Applying power rule of derivative,

`2y(dy)/(dt)+2x(dx)/(dt)=0`

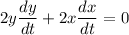
Simplifying,

`y(dy)/(dt)+x(dx)/(dt)=0`

Substituting the values,

`9(dy)/(dt)+12*1.5=0`

`9(dy)/(dt)+18=0`

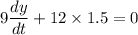
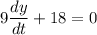
Subtracting both sides by 18,

`9(dy)/(dt)=-18`

Dividing both sides by 9,

`(dy)/(dt)= - 2`

Here, negative indicates that the ladder is sliding in downward direction.

`\therefore (dy)/(dt)= 2\:(ft)/(sec)`