Question

Using a linear approximation, estimate f(2.1), given that f(2) = 5 and f'(x) = √3x-1.

Answer 1

`f\left( {2.1} \right) \approx 5.22360`.

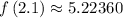Explanation:

The linear approximation is given by the equation

`{f\left( x \right) \approx L\left( x \right) }={ f\left( a \right) + f^\prime\left( a \right)\left( {x - a} \right).}`

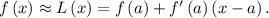
Linear approximation is a good way to approximate values of
`f(x)` as long as you stay close to the point
`x= a`, but the farther you get from
`x=a`, the worse your approximation.

We know that,

`a=2\\f(2) = 5\\f'(x) = √(3x-1)`

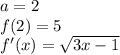
Next, we need to plug in the known values and calculate the value of
`f(2.1)`:

`{L\left( x \right) = f\left( 2 \right) + f^\prime\left( 2 \right)\left( {x - 2} \right) }=5+√(3(2)-1)(x-2) =5+√(5)(x-2)`

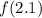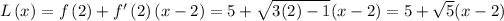
Then

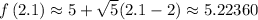`f\left( {2.1} \right) \approx 5+√(5)(2.1-2)\approx5.22360`.