Question

According to a 2014 Gallup poll, 56% of uninsured Americans who plan to get health insurance say they will do so through a government health insurance exchange.

a. What is the probability that in a random sample of 10 people exactly 6 plan to get health insurance through a government health insurance exchange?
b. What is the probability that in a random sample of 1000 people exactly 600 plan to get health insurance through a government health insurance exchange?
c. What are the expected value and the variance of X?
d. What is the probability that less than 600 people plan to get health insurance through a government health insurance exchange?

Answer 1

a) 24.27% probability that in a random sample of 10 people exactly 6 plan to get health insurance through a government health insurance exchange

b) 0.1% probability that in a random sample of 1000 people exactly 600 plan to get health insurance through a government health insurance exchange

c) Expected value is 560, variance is 246.4

d) 99.34% probability that less than 600 people plan to get health insurance through a government health insurance exchange

Explanation:

To solve this question, we need to understand the binomial probability distribution and the binomial approximation to the normal.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

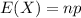
The variance of the binomial distribution is:

`V(X) = np(1-p)`

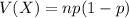
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

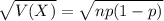
Normal probability distribution

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

When we are approximating a binomial distribution to a normal one, we have that
`\mu = E(X)`,
`\sigma = √(V(X))`.

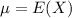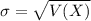56% of uninsured Americans who plan to get health insurance say they will do so through a government health insurance exchange.

This means that
`p = 0.56`

a. What is the probability that in a random sample of 10 people exactly 6 plan to get health insurance through a government health insurance exchange?

This is P(X = 6) when n = 10. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 6) = C_(10,6).(0.56)^(6).(0.44)^(4) = 0.2427`

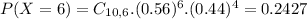
24.27% probability that in a random sample of 10 people exactly 6 plan to get health insurance through a government health insurance exchange

b. What is the probability that in a random sample of 1000 people exactly 600 plan to get health insurance through a government health insurance exchange?

This is P(X = 600) when n = 1000. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 600) = C_(1000,600).(0.56)^(600).(0.44)^(400) = 0.001`

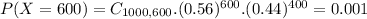
0.1% probability that in a random sample of 1000 people exactly 600 plan to get health insurance through a government health insurance exchange

c. What are the expected value and the variance of X?

`E(X) = np = 1000*0.56 = 560`

`V(X) = np(1-p) = 1000*0.56*0.44 = 246.4`

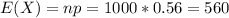
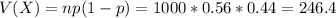
d. What is the probability that less than 600 people plan to get health insurance through a government health insurance exchange?

Using the approximation to the normal

`\mu = 560, \sigma = √(246.4) = 15.70`

This is the pvalue of Z when X = 600-1 = 599. Subtract by 1 because it is less, and not less or equal.

`Z = (X - \mu)/(\sigma)`

`Z = (599 - 560)/(15.70)`

`Z = 2.48`

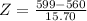
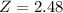
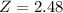`Z = 2.48` has a pvalue of 0.9934

99.34% probability that less than 600 people plan to get health insurance through a government health insurance exchange