Question

The scale on the ω axis is set by ωs = 6.0 rad/s. (a) What is the magnitude of the rod’s angular acceleration? (b) At t = 4.0 s, the rod has a rotational kinetic energy of 1.60 J. What is its kinetic energy at t = 0?

Answer 1

a. 1.5rad/s

b. 0.40J

Step-by-step explanation:

a. Angular acceleration is obtained by determining the gradient of the straight line.

-The graph perfectly cuts two points[4,4], [2,1]:

`Gradient=(\bigtriangleup y)/(\bigtriangleup x)\\\\=(4-1)/(4-2)\\\\=1.5`

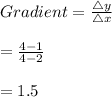
#The line's gradient is 1.5

Hence, the rod's angular acceleration is 1.5rad/s

b. Let at t=0, the angular velocity be
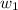`w_1` and
`w_2` at
`t=4`.

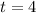#Rotational kinetic energy is determined using the formula:

`E_k=(1)/(2)m\omega^2r^2, r=radius`

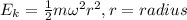
#Equate the expression to the energy value given:

`E_k=(1)/(2)m\omega_2^2r^2\\\\(1)/(2)m\omega_2^2r^2=1.60J, \ \omega_2=4\\\\(1)/(2)m* 4^2* r^2=1.60\\\\mr^2=0.20\\\\\# Taking \ x(t)=0->y(\omega_1)=-2\\\\\therefore E_k=0.5mr^2* \omega_1^2, \ \ \#t=0\\\\E_k=0.5* 0.2* (-2)^2\\\\=0.40`

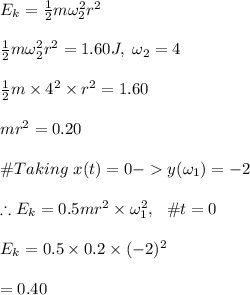
Hence, the kinetic energy at t=o is 0.40J