Question

The length of a rectangle is 4FT less than three times the width, and the area of the rectangle is 55FT. Find the dimensions of the rectangle.

Answer 1

• The required dimensions of rectangle are 11 feet and 5 feet.

Step-by-step explanation:

Given, The length of a rectangle is 4 ft less than three times the width, and the area of the rectangle is 55 ft².

Let's assume width of rectangle be x feet and length be 3x - 4 feet. Using the formula of Area of rectangle we'll find the value of length and width.

`\\ \dashrightarrow{ \red{ \underline{ \underline {\sf\: \:Area _((rectangle)) = Length * width}}}} \\ \\`

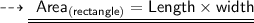
Substituting the required values:

`\dashrightarrow\: \: (3x - 4)(x) = 55 \\`

`\dashrightarrow\: \: 3x^2 - 4x = 55 \\`

`\dashrightarrow\: \: 3x^2 - 4x - 55 = 0 \\`

`\dashrightarrow\: \: 3x^2 + 11x - 15x - 55 = 0 \\`

`\dashrightarrow\: \: x(3x+11) -5(3x+11) = 0 \\`

`\dashrightarrow\: \: (x-5)(3x+11) = 0 \\`

`{ \red{ \dashrightarrow\: \: { \underline{ \underline{ {x = 5 \: or \: (-11)/(3)}}}}}} \\ \\`

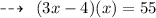
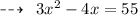
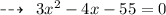
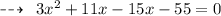
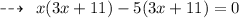
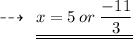
Hence,

• Length of rectangle = 3x - 4 = 3(5) -4 = 11 feet
• Breadth of rectangle= x = 5 feet

`\therefore` The required dimensions of rectangle are 11 feet and 5 feet.