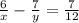Question

Two pipes are used to fill a 300-gallon tub with water. The wide pipe can fill the tub in x hours. The narrow pipe can fill the tub in twice the time. Unfortunately, there is a leak in the bottom of the tub that could drain a full tub in y hours. At the beginning of the day, the tub is empty. Then, both pipes are fully opened, and water is released for two hours before the pipes are shut off. The leak continues to drain the tub for three hours, at which point both of the pipes are reopened and allowed to run for another two hours. At that point, an attendant repairs the leak, closes the pipes, and measures the tub to be 712 full.

Answer 1

`(6)/(x)-(7)/(y)=(7)/(12)`

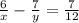
Explanation:

#We know that the filling taps will run for a cumulative 4hrs each while the draining hole will empty for a combined 7hrs.

Let x be the rate of the first filling tap, and 2x of the 2nd filling tap and y be the rate of the hole.

#The rate at which the tub fills per hour is :

`V_(tub)=(1)/(x)+(1)/(2x)-(1)/(y)\\\\=(1)/(x)(1+(1)/(2))-(1)/(y)\\\\=(3)/(2x)-(1)/(y)`

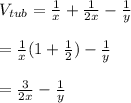
#The volume of the tub at the instant moment the leak is repaired is expressed as:

`V_(tub)=(3)/(2x)t_1-(1)/(y)t_2=(7)/(12), \ \ \ \ \ \ t_1=4,t_2=7\\\\\\(3)/(2x)* 4-(1)/(y)*7(7)/(12)\\\\\\(6)/(x)-(7)/(y)=(7)/(12)`

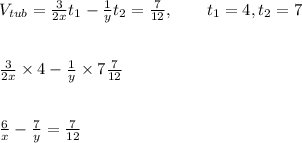
Hence, the volume of the tub after the leak is repaired is expressed as
`(6)/(x)-(7)/(y)=(7)/(12)`