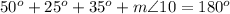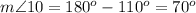Geometry- Finding Angles Can anyone help with this? - QAmmunity.org

Geometry- Finding Angles Can anyone help with this?

asked May 18, 2021 68.3k views

1 Answer

Answer:

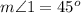
$m\angle 1=45^o$

$m\angle 2=75^o$

$m\angle 3=35^o$

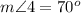
$m\angle 4=70^o$

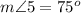
$m\angle 5=75^o$

$m\angle 6=55^o$

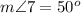
$m\angle 7=50^o$

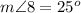
$m\angle 8=25^o$

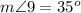
$m\angle 9=35^o$

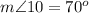
$m\angle 10=70^o$

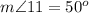
$m\angle 11=50^o$

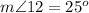
$m\angle 12=25^o$

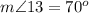
$m\angle 13=70^o$

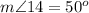
$m\angle 14=50^o$

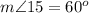
$m\angle 15=60^o$

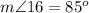
$m\angle 16=85^o$

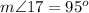
$m\angle 17=95^o$

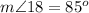
$m\angle 18=85^o$

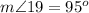
$m\angle 19=95^o$

Explanation:

step 1

Find the measure of arc FG

we know that

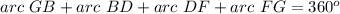$arc\ GB+arc\ BD+arc\ DF+arc\ FG=360^o$ ---> by complete circle

substitute the given values

$50^o+100^o+140^o+arc\ FG=360^o$

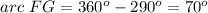
$arc\ FG=360^o-290^o=70^o$

step 2

Find the measure of angle 9

we know that

The inscribed angle is half that of the arc comprising

so

$m\angle 9=(1)/(2)[arc\ GF]$

we have

$arc\ FG=70^o$

substitute

$m\angle 9=(1)/(2)[70^o]=35^o$

step 3

Find the measure of angle 11

we know that

The inscribed angle is half that of the arc comprising

so

$m\angle 11=(1)/(2)[arc\ BD]$

we have

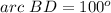
$arc\ BD=100^o$

$m\angle 11=(1)/(2)[100^o]=50^o$

step 4

Find the measure of angle 12

we know that

The inscribed angle is half that of the arc comprising

so

$m\angle 12=(1)/(2)[arc\ BG]$

we have

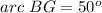
$arc\ BG=50^o$

$m\angle 12=(1)/(2)[50^o]=25^o$

step 5

Find the measure of angle 13

$m\angle 13=(1)/(2)[arc\ DF]$

we have

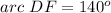
$arc\ DF=140^o$

$m\angle 13=(1)/(2)[140^o]=70^o$

step 6

Find the measure of angle 4

we know that

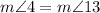$m\angle 4=m\angle 13$ ---> the inscribed angle has the same arc comprising DF

therefore

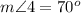
$m\angle 4=70^o$

step 7

Find the measure of angle 14

we know that

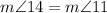$m\angle 14=m\angle 11$ ---> the inscribed angle has the same arc comprising BD

therefore

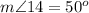
$m\angle 14=50^o$

step 8

Find the measure of angle 15

we know that

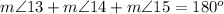$m\angle 13+m\angle 14+m\angle 15=180^o$ ---> by form a straight line

substitute the given values

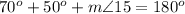
$70^o+50^o+m\angle 15=180^o$

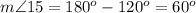
$m\angle 15=180^o-120^o=60^o$

step 9

Find the measure of angle 16

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

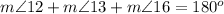
$m\angle 12+m\angle 13+m\angle 16=180^o$

substitute given values

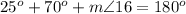
$25^o+70^o+m\angle 16=180^o$

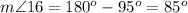
$m\angle 16=180^o-95^o=85^o$

step 10

Find the measure of angle 17

we know that

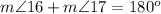$m\angle 16+m\angle 17=180^o$ ---> by form a straight line

substitute the given value

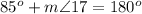
$85^o+m\angle 17=180^o$

$m\angle 17=180^o-85^o=95^o$

step 11

Find the measure of angle 18

we know that

$m\angle 18=m\angle 16$ ---> by vertical angles

therefore

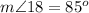
$m\angle 18=85^o$

step 12

Find the measure of angle 19

we know that

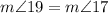$m\angle 19=m\angle 17$ ---> by vertical angles

therefore

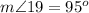
$m\angle 19=95^o$

step 13

Find the measure of angle 1

we know that

The measurement of the external angle is the half-difference of the arches that comprise

$m\angle 1=(1)/(2)[arc\ DF-arc\ GB]$

substitute

$m\angle 1=(1)/(2)[140^o-50^o]=45^o$

step 14

Find the measure of angle 3

we know that

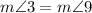$m\angle 3=m\angle 9$ ---> the inscribed angle has the same arc comprising BD

therefore

$m\angle 3=35^o$

step 15

Find the measure of angle 2

we know that

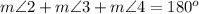$m\angle 2+m\angle 3+m\angle 4=180^o$ ---> by form a straight line

substitute the given values

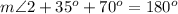
$m\angle 2+35^o+70^o=180^o$

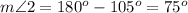
$m\angle 2=180^o-105^o=75^o$

step 16

Find the measure of angle 5

we know that

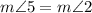$m\angle 5=m\angle 2$ ---> by vertical angles

therefore

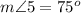
$m\angle 5=75^o$

step 17

Find the measure of angle 6

we know that

The measurement of the external angle is the half-difference of the arches that comprise

$m\angle 6=(1)/(2)[arc\ DFG-arc\ BD]$

substitute

$m\angle 6=(1)/(2)[210^o-100^o]=55^o$

step 18

Find the measure of angle 8

we know that

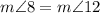$m\angle 8=m\angle 12$ ---> the inscribed angle has the same arc comprising GB

therefore

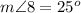
$m\angle 8=25^o$

step 19

Find the measure of angle 7

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

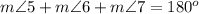
$m\angle 5+m\angle 6+m\angle 7=180^o$

substitute

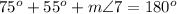
$75^o+55^o+m\angle 7=180^o$

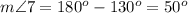
$m\angle 7=180^o-130^o=50^o$

step 20

Find the measure of angle 10

we know that

$m\angle 7+m\angle 8+m\angle 9+m\angle 10=180^o$ ---> by form a straight line

substitute

$50^o+25^o+35^o+m\angle 10=180^o$

$m\angle 10=180^o-110^o=70^o$

Watcom answered May 24, 2021

by Watcom

4.7k points

Search QAmmunity.org