Answer:
Part 1)
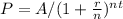 (see the explanation)
(see the explanation)
Part 2)
![r=n[(A)/(P)^(1/(nt))-1]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ixf3plnjo7caui9b8w5rnbzlzikgy0y65e.png) (see the explanation)
(see the explanation)
Part 3)
![t=log((A)/(P))/[(n)log(1+(r)/(n))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8a6mx0yj0fp1e6hnmcls19dkdtxuh8kzwl.png) (see the explanation)
(see the explanation)
Explanation:
we know that
The compound interest formula is equal to
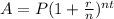
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
Part 1) Find the Principal P
The values of A,r,n and t are given
Isolate the variable P
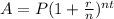
Divide both side by
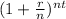
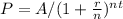
Part 2) Find the rate r
The values of A,P,n and t are given
Isolate the variable r
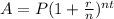
Divide both sides by P
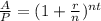
Elevated both sides to 1/(nt)
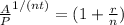
subtract 1 both sides

Multiply by n both sides
![r=n[(A)/(P)^(1/(nt))-1]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ixf3plnjo7caui9b8w5rnbzlzikgy0y65e.png)
Part 3) Find the time t
The values of A,P,r and n are given
Isolate the variable t
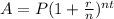
Divide both sides by P
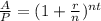
Apply log both sides
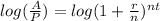
Apply property of exponents

Divide both side by
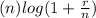
![t=log((A)/(P))/[(n)log(1+(r)/(n))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8a6mx0yj0fp1e6hnmcls19dkdtxuh8kzwl.png)