Question

Suppose the lengths of two sides of a right triangle are represented by 2x and 3 (x + 1), and the longest side is 17 units. Find the value of x.

Answer 1

x = 4

Explanation:

The length of two legs of a right angle triangle are 2x and 3(x+1).

The length of longest side is 17 units. It means measure of hypotenuse is 17 units.

According to the pythagoras theorem,

`leg_1^2+leg_2^2=hypotenuse^2`

`(2x)^2+(3(x+1))^2=(17)^2`

`4x^2+9(x^2+2x+1)=289`

`4x^2+9x^2+18x+9=289`

`13x^2+18x-280=0`

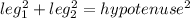
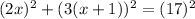
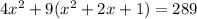
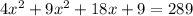
On splitting the middle terms we get

`13x^2+70x-52x-280=0`

`x(13x+70)-4(13x+70)=0`

`(13x+70)(x-4)=0`

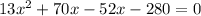
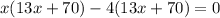
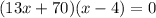
Using zero product property we get

`13x+70=0\Rightarrow x=-(70)/(13)`

`x-4=0\Rightarrow x=4`

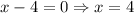
The value of x can not be a negaive number, because for negative value of x the value of 2x is negative and side can not be negative.

Therefore, the value of x is 4.

Answer 2

x=4

Explanation:

Step 1:-

given the lengths of two sides of a right angle are represented by 2x and 3(x+1) and longest side is 17 units.

AB = 2x and BC = 3(x+1) and longest side AC= 17

by using Pythagoras theorem

`AC^2 = AB^2 + BC^2`

step 2:-

The hypotenuse is longest side is AC = 17 units

(17)^2 = 4x^2 +9(X+1)^2

on simplification, we will use formula

`(a + b)^2 = a^2 +2ab+b^2`

289 = 4x^2 +9(x^2+2x+1)

`13x^2 +18x-280 = 0`

finding factors 70 X 52 = 3640

`13x^2 +70x-52x-280 = 0`

`13x^2 -52x+ 70x-280 = 0`

Taking common , we get

13x(x-4)+70(x-4)=0

x-4=0 and 13x+70=0

x=4 and
`13x =-70`

x=4 and
`x=(-70)/(13)`

we can not choose negative value so x value is 4

Final answer:- x = 4

verification:-

`AC^2 = AB^2 + BC^2`

289 = 4(4)^2+9(4+1)^2

289 = 64 +9(25)

289=289