Question

Given the lengths of two sides of a triangle, find the range for the length of the third side (between what two numbers should the length of the third side be). Write the inequalities for each case.

13.2 and 6.7

Answer 1

The length of the third side of given triangle lies between 6.5 and 19.9.

Explanation:

The law of cosine is as follows

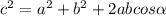`c^(2) =a^(2)+b^(2)+2abcos\alpha`---------------1

⇒ a and b are the given sides of the triangle and c is the third side, and
`\alpha` is the angle between a and b .

In equation 1 , the maximum and minimum values of
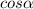`cos\alpha` are 1 and -1.

so the value of c lies in between

⇒
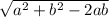`\sqrt{a^(2)+b^(2)-2ab }` and
`\sqrt{a^(2)+b^(2)+2ab }` =
`|a-b| and |a+b|`

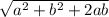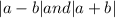
Given a=13.2 and b=6.7 so the the side lies in between |13.2-6.7| and |13.2+6.7|

so the third side lies between 6.5 and 19.9