Question

(1 point) The time rate of change of a rabbit population P is proportional to the square root of P. At time t=0 (months) the population numbers 100 rabbits and is increasing at the rate of 10 rabbits per month. Let P′=kP12 describe the growth of the rabbit population, where k is a positive constant to be found. Find the formulas for k and for the rabbit population P(t) after t months.

Answer 1

2√P = t + 20

Explanation:

Rate of change of a rabbit population ∝ √P

`(dP)/(dt)=k√(P)`

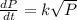
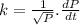`k=(1)/(√(P)).(dP)/(dt)` -----(1)

At time 't' = 0 the population of the rabbits (P) = 100 and
`(dP)/(dt)=10` rabbits per month.

We plug in the values in the equation (1),

`k=(1)/(√(100))* 10`

k = 1

Equation (1) becomes,
`(dP)/(dt)=1* √(P)`

`(dP)/(√(P))=dt`

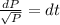
By the integration of this equation,

`\int (dP)/(√(P))=\int dt`

`(√(P))/((1)/(2))=t+C`

`2√(P)=t+C`

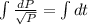
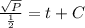
Again for t = 0 and P = 100,

`2√(100)=0+C`

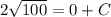
C = 20

Now the integrated equation will be,

`2√(P)=t+20`

Therefore, formula representing population P after time t is,

2√P = t + 20