Question

A 2.37-F and a 5.36-F capacitor are connected in series across a 40.0-V battery. A 8.45-F capacitor is then connected in parallel across the 2.37-F capacitor. Determine the voltage across the 8.45-F capacitor.

Answer 1

The voltage across the 8.45F capacitor is 27.73 Volts

Step-by-step explanation:

Given that,

A 2.37-F and a 5.36-F capacitor are connected in series across a 40.0 V battery,

`C_(1)=2.37 F\\C_(2)=5.36 F\\V = 40.0 V`

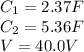
To Find:

V₁ = ? (voltage across the 10.00 µF capacitor)

Solution:

For Capacitor Series Combination we have

`(1)/(C_(s))=(1)/(C_(1))+(1)/(C_(2))`

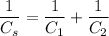
Substituting the values we get

`(1)/(C_(s))=(1)/(2.37)+(1)/(5.36)\\C_(s)=1.643F`

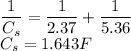
As Capacitors are connected in series they have the same charge on each plates, and is given by,

`Q= C_(s)* V`

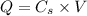
Substituting the values we get

`Q= 1.643 F* 40\\=65.72C\\Q=65.72 C`

Also in Series voltage will be different across C₁ and C₂,

Therefore voltage across C₁ will be

`V_(1)= (Q)/(C_(1))`

Substituting the values we get

`V_(1)=(65.72)/(2.37)=27.73\ Volt`

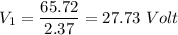
Now according to the given condition,

8.45F capacitor is then connected in parallel across the 2.37 F capacitor,

Therefore we know in Parallel, Voltage remain Same, Hence Voltage across 8.45F capacitor will be same as that of voltage across V₁.

Hence,

The voltage across the 8.45F capacitor is 27.73 Volts